구조역학이나 재료역학에서 초반부에 배우는 단순보의 지점 반력과 부재력도의 작성 방법에 대해서
알려드리려고 합니다.
단순보 대칭일 경우

위의 그림1과 같은 단순보에서 A점과 B점의 반력을 구하기 위해선 평형조건식으로
$\Sigma H=0$, $\Sigma V=0$, $\Sigma M=0$의 3개의 방정식을 구할 수 있습니다. (H=수평력, V=수직력, M=휨모멘트)
그림1의 단순보의 경우 미지수가 $V_{A}, V_{B}$ 2개이므로 평형조건식 $\Sigma V=0$, $\Sigma M=0$, 2개의 방정식을 이용하여 구해도 되지만 좌우대칭이기 때문에 $\Sigma V=0$을 이용히 1개의 방정식으로 각 지점의 반력을 구할 수 있습니다.
※ 부호의 기준은 다를 수 있지만 여기서는
수평력 : → 방향은 (+) / ← 방향은 (-)
수직력 : ↑ 방향은 (+) / ↓ 방향은 (-)
휨모멘트 : ↻ 방향은 (+) / ⟲ 방향은 (-) 로 정하겠습니다.
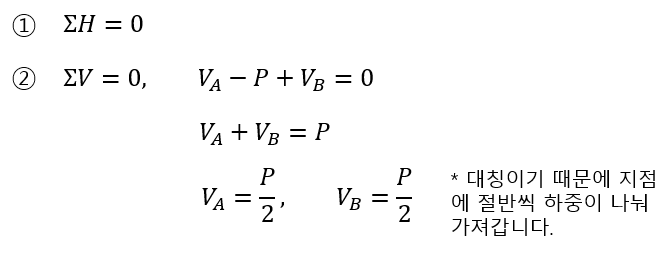
그림2와 같이 지점의 반력을 구했다면 SFD(전단력도), BMD(휨모멘트도)를 작성할 준비가 되었습니다.

SFD(전단력도)의 경우 왼쪽 A지점에서부터 지점반력인 $\dfrac{P}{2}$의 값만큼 올라간 뒤 외력이 존재하는 $\dfrac{L}{2}$ 부분에서 -P만큼 내려갑니다. 이후 B지점에서 지점 반력인 $\dfrac{P}{2}$ 의 값만큼 올라가서 그림3과 같은 부재력도가 완성됩니다.

그림4와 같이 BMD는 전단력도의 면적과 관련이 있습니다. 외력이 발생하여 전단력도의 크기가 변화되는 구간까지의 면적을 구하게 되면 $M_{max}=M_{L/2}=V_{L/2} \times \dfrac{L}{2}=\dfrac{PL}{4}$로 구할 수 있습니다.

따라서 단순보의 부재력도는 그림5와 같이 작성하시면 됩니다.
부재의 중앙부 집중하중시 공식
$V_{A}, V_{B} = \dfrac{P}{2}$
$M_{max} = \dfrac{PL}{4}$
'건축직 공기업 필기 기출 > 이론' 카테고리의 다른 글
| 철근콘크리트에서 최소철근비와 최대철근비에 대해서,,, (1) | 2024.03.06 |
|---|---|
| 설계하중에서 고정하중과 활하중에 대하여 (단위 정리) (0) | 2024.03.02 |
| 설계하중의 종류와 하중조합에 대해서 (1) | 2024.02.26 |
| 철근콘크리트 단근보 설계휨강도 구하기! (0) | 2024.02.24 |
| 단순보의 지점 반력 및 부재력도 작성 방법!!(하중 비대칭일 경우) (0) | 2024.02.20 |